Quelques nombres intéressants

Cette section parle de certains nombres qui ont des propriétés ou des fonctions intéressantes.

Pi:

Plusieurs le connaissent, certains savent comment s'en servir mais très peu, moi inclus, savent l'étendu de ses capacités. Pi, au départ est la constante qui résulte de la division de la circonférence d'un cercle par son diamètre. Pi peut apparaître dans d'autres problèmes et théories comme une qui veut que si l'on prends la longeur d'une rivière pour la diviser avec la longeur en ligne droite du début et de la fin d'une rivière nous obtiendrions à peu près Pi. L'explication de la théorie est que les rivières à cause de l'érosion vont creuser les parois de la rivière ce qui va accentuer les courbes mais les courbes trop accentuées vont re devenir une ligne droite. La moyenne de ses courbures donnant environ Pi.*https://en.wikipedia.org/wiki/Meander_cutoff#mediaviewer/File:OxbowAnimation.gif 

Pi, avec sa popularité, en vient même à inspirer quelques-uns à faire des oeuvres d'arts s'inspirant des décimales de Pi. Vous pouvez les regarder à ce site: https://mkweb.bcgsc.ca/pi/art/.

Bien entendu, décrire tout ce que Pi peut faire me prendrait environ 314159265 pages d'écriture tellement il est polivalent alors je vous laisse le soin de découvrir de quoi il est capable.

 

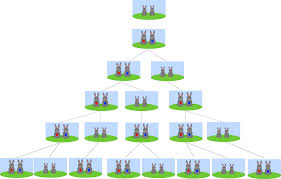
La suite de Fibonacci:

1,1,2,3,5,8,13,21... Séparément, ces nombres peuvent sembler anodins mais mis dans cet ordre, ils renferment de bien drôles de propriétés. Premièrement, il est important de savoir la logique derrière cette suite. En gros, chaque nombre de cette suite est la somme des deux d'avant. Donc ça commence avec 1 suivi de 1 (1+0=1), 2 (1+1=2), de 3 (1+2=3), de 5 (2+3=5) et ainsi de suite. Mais en quoi cette suite est elle intéressante?. Elle a un rapport étroit avec la nature. La très grande majorité des fleurs ont un nombre de pétales égal à un nombre de la suite de Fibonacci. La raison étant que ces nombres offrent un certain hermetisme permettant aux fleurs de mieux ce développer. Ce nombre se trouve dans d'autres domaines de la nature tel la reproduction des lapins.**

 

Phi (1.6180339887498948482...):

Phi ou le nombre d'or est un nombre étroitement lié à la suite de Fibonacci la raison étant qu'à chaque fois que l'on divise un des nombres de Fibonacci par le nombre qui le précède dans la suite la réponse va ressembler au nombre d'or et à mesure que l'on vance dans la suite, plus près nous serons du nombre d'or. Mais qu'a t'il de si spécial? Il est beau. Il est tout simplement agréable à regarder. Les proportions qu'il offre sont harmonieuses. Si l'on dessine un rectangles avec 1 de longueur et phi de largeur nous obtiendrons le rectangle d'or, nommé ainsi car il a des proportions agréables et donne un rectangle ni trop gros ni trop petit. Une autre forme appelée la spirale d'or est formé est séparant le rectangle d'or en deux parties, un carré 1 par 1 et un plus petit rectangle d'or et de faire cela à l'infini.**

Exemple rectangle d'or:                                                Exemple spirale d'or:

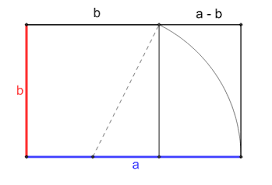
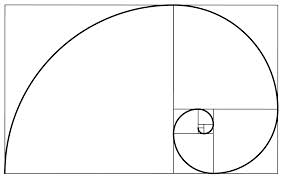
Phi est aussi très présent dans l'anatomie. Même si le corps humain n'est jamais pareil d'une personne à l'autre plusieurs croient qu'il est lié au nombre d'or. L'homme de Vitruve par exemple partage ces proportions et est pour plusieurs, le corps parfait. Certains voient même le nombre d'or dans l'architecture jusque dans le Parthénon.** L'opinion sur Phi est mitigée. Certains voient en lui la proportion divine d'autres la trouve complètement sans intérêt. Le choix est à vous.

Bien entendu, plusieurs autres nombres sont intéressant et méritent d'être étudié. Je n'ai parlé de ''e'', ''i'' etc. Qui sait, peut-être trouveras-tu des nombres aux propriétés étranges.

 

*https://www.sciencemag.org/content/271/5256/1710.abstract